6 Essential Types Of Algorithms For Coding Interviews

Algorithms are a set of steps or instructions that are designed to perform a specific task or action, primarily to solve a problem. Your ability to create correct and efficient algorithms is evaluated within software engineer coding interviews because companies like Google, Amazon, and Microsoft want to hire software engineers who deeply understand algorithms.

If you want to pass coding interviews that have problems that are designed around common data structures and algorithms, then you’ll want to make sure you understand what the most important types of algorithms are for you to study.

The most 6 important types of algorithms to study for coding interviews include sorting algorithms (i.e., bubble sort and heap sort), searching algorithms (i.e. the linear search algorithm), recursive algorithms (i.e. recursively implementing backtracking and dynamic programming algorithms), tree traversal algorithms (i.e. pre-order, in-order, and post-order traversals), graph algorithms (i.e. depth-first search and breadth-first search), and sliding window algorithms (i.e. variable sliding window algorithms).

In the rest of the article below, we will elaborate on the specific most important algorithms that you should know for solving technical interview questions, based on these essential types of algorithms. We will also discuss additional strategies at the end for passing coding interviews like practice questions online and learning about the most important data structures.

1. Sorting Algorithms

Sorting algorithms are types of algorithms that sort a list of sortable data (like primitives, numbers, and objects) into a logical ascending or descending order. Sorting algorithms are important to fundamentally understand in terms of time-space complexity for coding interviews because they are the basis of advanced algorithms that are used to solve interview questions optimally and serve as the easiest algorithms to comprehend in terms of understanding time and space complexity as a topic.

The 6 most important sorting algorithms to learn for coding interviews are listed below, along with a description of each of the sorting algorithms.

• Selection Sort: This sorting algorithm iteratively selects the smallest (or largest) element from the unsorted section of a list and swaps it with the first unsorted element. It extends the sorted sections one by one until the entire list is sorted.
• Bubble Sort: This sorting algorithm repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. This process is repeated until no swaps are needed, indicating the list is sorted.
• Insertion Sort: Starting from the second element of a list, this algorithm compares the current element with the previous elements and inserts it in its correct position among the already sorted elements, repeating this process for each element in the list.
• Merge Sort: This algorithm recursively divides a list into two halves until each sub-list contains a single element. After, each of the sub-lists is merged back together in a sorted manner, combining pairs of sub-lists until the original list is reformed in sorted order.
• Quick Sort: In this sorting algorithm, an element called the ‘pivot’ is chosen from the list and elements are partitioned into two sub-lists, one with elements less than the pivot and the other with elements greater than the pivot. This process is recursively applied to the sub-lists.
• Heap Sort: This sorting algorithm converts the list data structure into a binary heap structure that can be used to return either all the max elements or min elements in either ascending or descending order.

The table below depicts the worst-case time and space complexities of each of these important sorting algorithms.

Algorithm	Worst-Case Time Complexity	Space Complexity
Selection Sort	O(n^2)	O(1)
Bubble Sort	O(n^2)	O(1)
Insertion Sort	O(n^2)	O(1)
Merge Sort	O(n log n)	O(n)
Quick Sort	O(n^2) (rarely) or O(n log n)	O(log n)
Heap Sort	O(n log n)	O(1)

2. Searching Algorithms

Searching algorithms are types of algorithms that are used to search for, find, or retrieve an element within a collection of data (like a list, tree, or graph). This is one of the most common types of algorithms that are used in different variations throughout the vast majority of coding interview problems in conjunction with other algorithms.

There are 2 main categories of search algorithms that are used for solving interview problems. The two main categories of searching algorithms are linear (sequential) search and interval (binary) search.

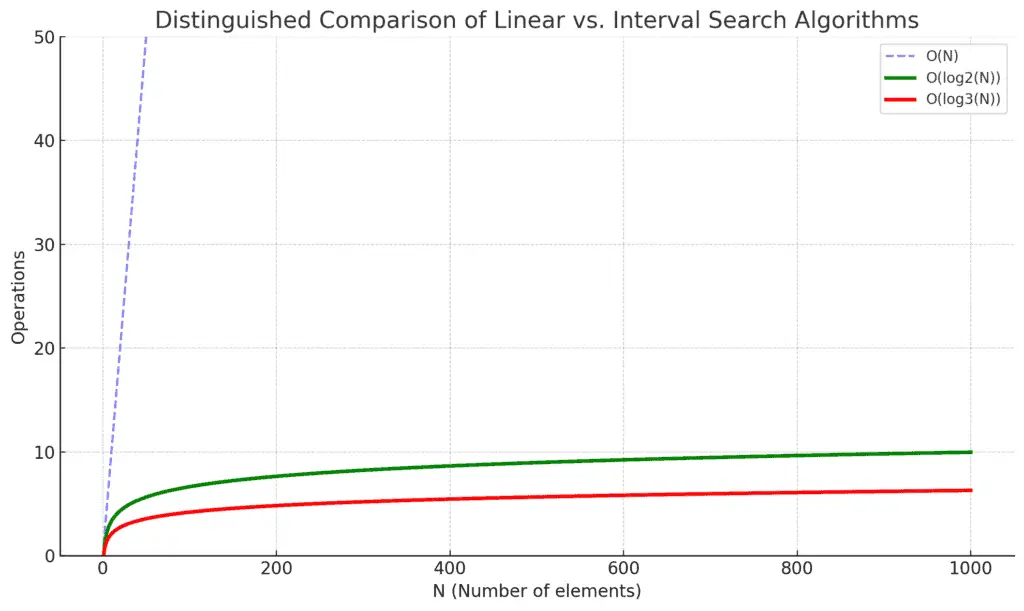
The chart below depicts a comparison in worst-case time complexity between one sequential and 2 interval search algorithms.

What Is A Linear Search Algorithm (Sequential Search)?

A linear search algorithm (also known as a sequential search algorithm) is a search algorithm that iterates through a sorted or unsorted collection of elements to find a specific element, by checking one element at a time. This is the most common type of search algorithm because it’s used, often unknowingly to the programmer, in control structures such as while loops and for loops.

A linear search algorithm has a worst-case time complexity of O(N) where N is the number of elements within a collection of elements. This is because you may have to iterate over N elements, in the worst case.

What Is A Interval Search Algorithm (Binary Search)?

An interval search algorithm is a type of algorithm that’s used to search through a sorted collection of elements for an element in a more time-complexity efficient way compared to a linear search. It achieves this by dividing the search space into 2 or more sections.

The binary search algorithm (also known as the half-interval search and logarithmic search) is a type of interval search that divides the search space into 2 sections at each step in the search algorithm. The binary search algorithm has a worst-case time complex of O(log₂(N)), where N is the number of elements in the collection, which is more efficient than the linear search algorithm.

3. Recursive Algorithms

A recursive algorithm is a type of algorithm that continually calls itself with input values that allow it to converge either to a value or a program execution state. Every algorithm that can be written recursively, can also be written in a way that doesn’t require recursion (also known as “iterative solutions”). However, typically, recursive algorithms are easier to implement solutions in than their non-recursive solutions.

Recursive algorithms are common for many coding interview problems that require advanced algorithms such as divide and conquer algorithms, dynamic programming algorithms, and backtracking algorithms.

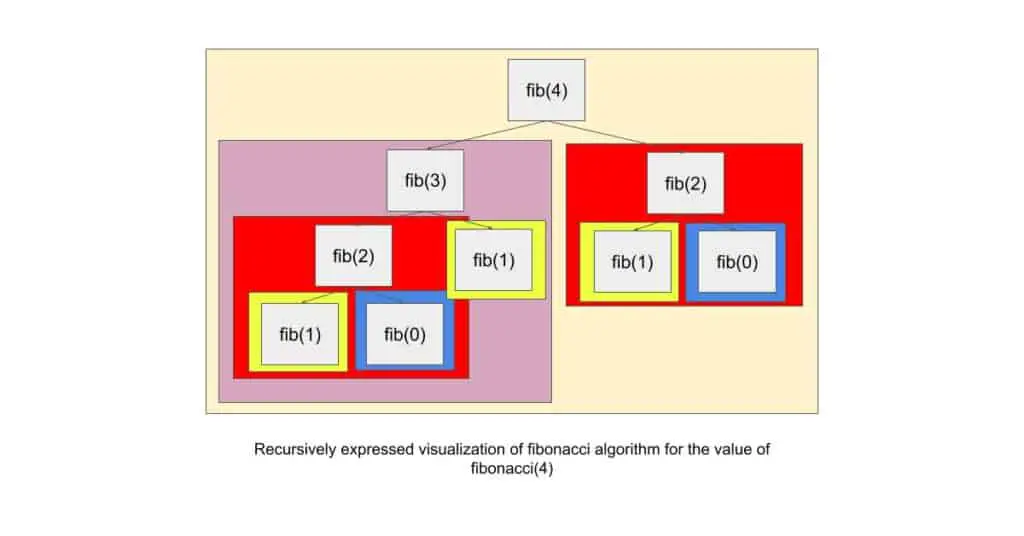
The image below visually expresses what a recursive algorithm looks like with the Fibonacci algorithm.

What Are Divide And Conquer Algorithms?

Divide and conquer algorithms are types of algorithms that are used to solve complex problems by breaking them down into the three distinct steps of dividing (creating sub-problems from the original problem), conquering (solving the smallest sub-problems first), and combining (solving the next sets of sub-problems using the already solved sub-problems, until you solve the original problem). Divide and conquer algorithms are typically implemented with recursive algorithms.

Examples of divide and conquer algorithms include quick sort and merge sort.

What Are Dynamic Programming Algorithms?

Dynamic programming (often abbreviated as DP) algorithms are types of algorithms that are used for solving complex problems by dividing the problem into smaller subproblems to solve while not repeating duplicated computations. This is achieved through techniques such as memoization and tabulation, which cache data into data structures and help improve the time complexity of DP algorithms.

Recursion, as a topic, is tied to dynamic programming algorithms because it is often used as the basis for DP solutions. Often, dynamic programming algorithms use recursion as well, so it’s important to understand both recursive and dynamic programming algorithms to pass coding interviews.

What Are Backtracking Algorithms?

Backtracking algorithms are types of algorithms that do a “trial-and-error-based” approach to execution by attempting to traverse a path (in a data structure like a graph or matrix) until blocked, and then retracing steps in the path until a new path can be explored. Often, backtracking algorithms are implemented with recursive algorithm implementations. 

4. Tree Traversal Algorithms

Tree traversal algorithms are algorithms that allow you to traverse the nodes of a tree data structure in a specific order. The 4 main ways of traversing a tree’s nodes are through pre-order traversal, in-order traversal, post-order traversal, and level-order traversals. These algorithms are important to know because tree traversal algorithms are common solutions to the majority of coding interview problems that have a tree data structure.

While the 4 main ways of traversing a tree are used primarily on binary trees in interview problems, it’s important to understand that these traversals work for any n-ary tree (a tree data structure with an arbitrary number of child nodes per parent node). However, there is no universally accepted way of doing in-order traversal on n-ary trees where the n (in the n-ary tree) is greater than 2.

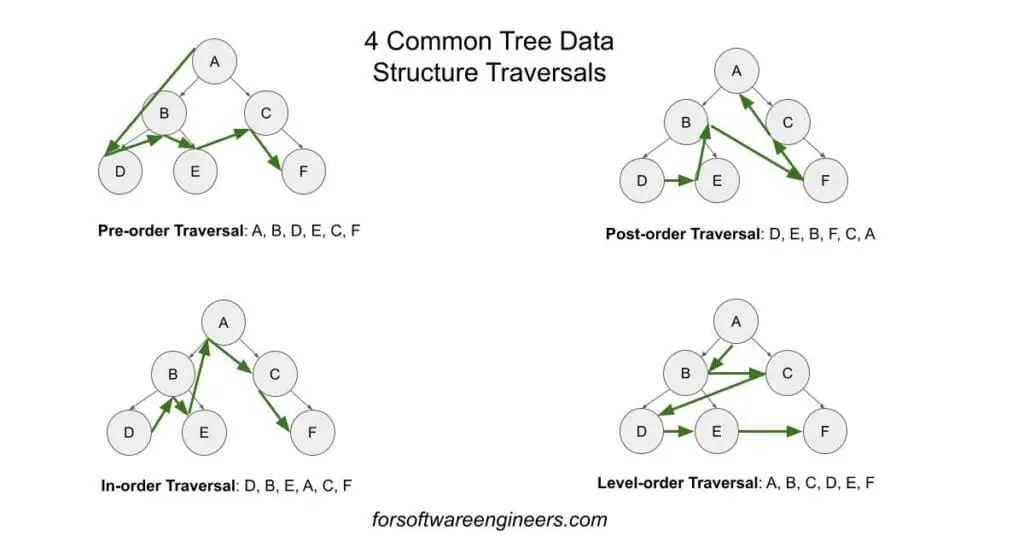
The below below shows what each tree traversal algorithm looks like.

What Is The Pre-Order Traversal Algorithm?

The pre-order tree traversal algorithm is a way of traversing through the elements of a tree data structure in a way that you visit and process nodes recursively in a middle node and then child nodes (from left-most to right-most) methodology. 

What Is The In-Order Traversal Algorithm?

The in-order tree traversal algorithm is a way of traversing through the elements of a binary tree data structure in a way that you visit and process nodes recursively in a left child-node, middle-node, then right child-node methodology. There is no consensus on how to do this for a n-ary tree where n is greater than 2.

What Is The Post-Order Traversal Algorithm?

The post-order tree traversal algorithm is a way of traversing through the elements of a tree data structure in a way that you visit and process nodes recursively in child nodes (from left-most to right-most) and then middle node methodology. 

What Is The Level-Order Traversal Algorithm?

The post-order tree traversal algorithm is a way of traversing through the elements of a tree data structure in a way that you visit and process nodes from top to bottom, from left to right, similar to how you would read the pages of a book written in America.

5. Graph Algorithms

Graph algorithms are types of algorithms that are used to traverse or search for nodes within a network-like structure like a maze implemented as a multi-dimensional array or graph data structure. The three main types of graph algorithms are depth-first search, breadth-first search, and Djkstra’s algorithm. These types of graph algorithms are used to solve interview problems related to traversing a graph, finding a node in a graph, detecting cycles in a graph, and finding the shortest path between two nodes in a graph.

Many of the solutions to coding interview problems require graph algorithms to solve efficiently, so graph algorithms are important to learn and understand. 

Examples of when you would use each of these graph algorithms are listed below.

• Examples To Use Depth-First Search (DFS)
  • Detecting a cycle in a directed graph by marking nodes and keeping track of the current processing path
  • Finding a path from source to destination in a maze by traversing through a maze represented as a 2D array
  • Topological sorting of a directed acyclic graph to find a linear ordering of its vertices such that for every directed edge UV from vertex U to vertex V, U comes before V in the ordering
• Examples To Use Breadth-First Search (BFS)
  • Finding the shortest path between two nodes in an unweighted graph using BFS to traverse and measure distances
  • Level order traversal in trees where all nodes at depth d are processed before nodes at depth d+1
  • Finding the connected components of an undirected graph to identify separate islands or sub-graphs within a larger undirected graph
• Examples To Use Dijkstra’s Algorithm
  • Finding the shortest path from a source to all other vertices in a weighted graph by evaluating and updating path costs
  • Routing in computer networks to determine the optimal path for data packets between two nodes in a network
  • Traffic navigation systems to suggest the shortest or quickest route between two locations on a map based on current traffic conditions

What Is The Depth-First Search (DFS) Algorithm?

The depth-first search (abbreviated as DFS) algorithm is an algorithm that explores nodes within a graph-like structure by starting from a source node and recursively exploring child nodes it hasn’t visited before backtracking. The algorithm’s search explores as deep as it can before trying any other path.

What Is The Breadth-First Search (BFS) Algorithm?

The breadth-first search (abbreviated as BFS) algorithm is an algorithm that explores nodes within a graph-like structure by exploring nodes in a level-by-level order. This is especially useful for finding the shortest path in an unweighted graph.

What Is Djkstra’s Algorithm (Shortest Path Algorithm)?

Dijkstra’s algorithm is an algorithm that reveals the shortest path within a weighted graph. It uses a priority queue data structure to select the next closest node and it is efficient in graphs that don’t have negative weight edges.

6. Sliding Window Algorithms

Sliding window algorithms are types of algorithms that are used to solve string, array, and list-based problems optimally. These algorithms involve maintaining the state based on a “window” or group of values that moves across indices and values of a data structure (like a string, array, or list). A key indicator that a sliding window algorithm is an optimal solution to a coding interview problem is when the problem asks for either a “maximum”, “minimum”, “longest”, or “shortest” amount of value across contiguous subarrays or substrings of a given size.

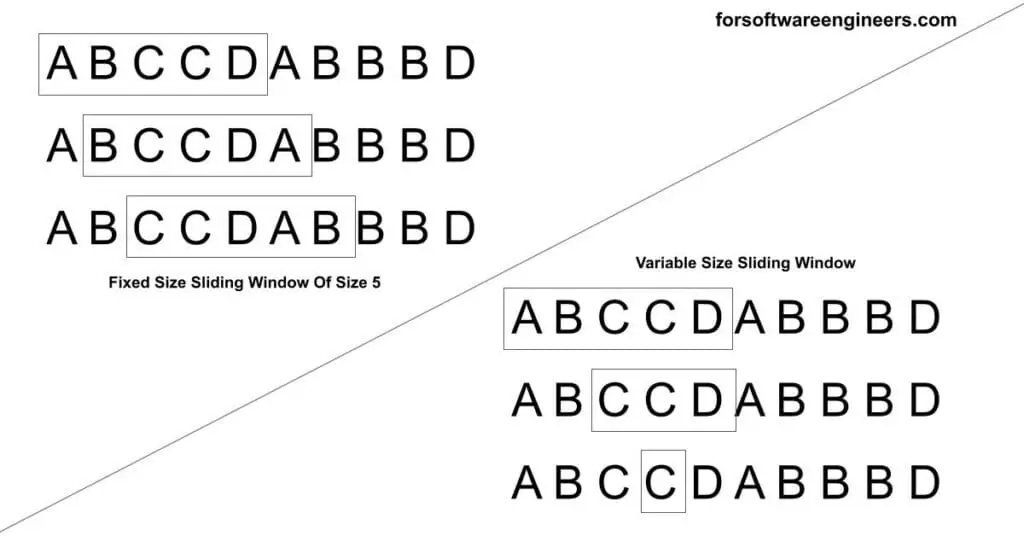
The two types of sliding window algorithms are fixed sliding windows and variable sliding windows. Fixed sliding window algorithms use groups or windows of a fixed size throughout an algorithm. Variable sliding window algorithms use groups or windows of a variable size throughout an algorithm. Visual examples of these types of sliding window algorithms are shown in the image below.

How Do You Prepare For Algorithm-Focused Coding Interviews?

You prepare for algorithm-focused coding interviews by practicing coding interview questions that are related to both data structures and algorithms. Knowledge of common data structures and algorithms is an essential aspect of solving coding interview problems and passing coding interviews. 

What Are The Best Sites To Practice Algorithm Coding Interview Practice Problems

The best websites to practice algorithm coding interview problems include websites like LeetCode and HackerRank. Both of these websites allow you to practice the most relevant coding interview questions for coding interviews for free on their online coding platforms which also provide tests for your solutions. 

How Important Is Studying Data Structures With Algorithms?

It is very important to study data structures with algorithms because they’re both used together within coding interview questions. There are 9 most important data structures to study for coding interviews which include strings, arrays, hash tables, stacks, queues, linked lists, trees, heaps, and graphs.
Studying each of these data structures (with algorithms), understanding their use cases, and knowing how and when to apply them will improve your chances of passing the vast majority of coding interviews. These data structures are the 9 most important data structures to study for a coding interview because they’re the most common data structures that are used in optimal solutions for coding interview problems.